Working Papers
- “Structural counterfactual analysis in macroeconomics: theory and inference” sole author, September 2024, 78 pages. (Job Market Paper) arXiv
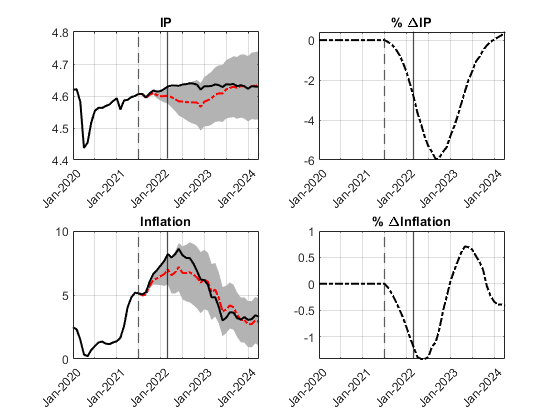
We propose a structural model-free methodology to analyze two types of macroeconomic counterfactuals related to policy path deviation: hypothetical trajectory and policy intervention. Our model-free approach is built on a structural vector moving-average (SVMA) model that relies solely on the identification of policy shocks, thereby eliminating the need to specify an entire structural model. Analytical solutions are derived for the counterfactual parameters, and statistical inference for these parameter estimates is provided using the Delta method. By utilizing external instruments, we introduce a projection-based method for the identification, estimation, and inference of these parameters. This approach connects our counterfactual analysis with the Local Projection literature. A simulation-based approach with nonlinear model is provided to add in addressing Lucas’ critique. The innovative model-free methodology is applied in three counterfactual studies on the U.S. monetary policy: (1) a historical scenario analysis for a hypothetical interest rate path in the post-pandemic era, (2) a future scenario analysis under either hawkish or dovish interest rate policy, and (3) an evaluation of the policy intervention effect of an oil price shock by zeroing out the systematic responses of the interest rate.
‘‘Simple robust two-stage estimation and inference for generalized impulse responses and multiple-horizon causality’’ with Jean-Marie Dufour (McGill University). September 2024, 106 pages. arXiv
This paper introduces a novel two-stage estimation and inference procedure for generalized impulse responses (GIRs). GIRs encompass all coefficients in a multi-horizon linear projection model of future outcomes of y on lagged values (Dufour and Renault, 1998), which include the Sims’ impulse response. The conventional use of Least Squares (LS) with heteroskedasticity- and autocorrelation-consistent covariance estimation is less precise and often results in unreliable finite sample tests, further complicated by the selection of bandwidth and kernel functions. Our two-stage method surpasses the LS approach in terms of estimation efficiency and robustness in finite-sample tests. The robustness stems from our proposed covariance matrix estimates, which eliminate the need to correct for serial correlation in the multi-horizon projection residuals. Our method accommodates non-stationary data and allows the projection horizon to grow with sample size. Monte Carlo simulations demonstrate our two-stage method outperforms the LS method. We apply the two-stage method to investigate the GIRs, implement multi-horizon Granger causality test, and find that economic uncertainty exerts both short-run (1-3 months) and long-run (30 months) effects on economic activities.‘‘Inference in High-Dimensional Linear Projections: Multi-Horizon Granger Causality and Network Connectedness’’ with Eugène Dettaa (Université de Montréal). September 2024, 57 pages.
arXiv
This paper presents a Wald test for multi-horizon Granger causality within a high-dimensional sparse Vector Autoregression (VAR) framework. The null hypothesis focuses on the causal coefficients of interest in a local projection (LP) at a given horizon. Nevertheless, the post-double-selection method on LP may not be applicable in this context, as a sparse VAR model does not necessarily imply a sparse LP for horizon h > 1. To validate the proposed test, we develop two types of de-biased estimators for the causal coefficients of interest. The first estimator is derived from the Least Squares method, while the second is obtained through a two-stage approach that offers potential efficiency gains. We further derive heteroskedasticity- and autocorrelation-consistent (HAC) inference for each estimator. As HAC correction for serial correlation performs poorly in small samples, we propose a robust inference method for the two-stage estimator, eliminating the need to correct for serial correlation in the projection residuals. Monte Carlo simulations show that the two-stage estimator with robust inference outperforms the Least Squares method, particularly for longer projection horizons. We apply our methodology to test both short-run and long-run Granger causality between country-level economic uncertainty measures and to visualize network connectedness across horizons. Our empirical findings reveal that the U.S. Granger-causes China in the short run (1 and 3 months), while China influences the U.S. in the long run (9 and 12 months).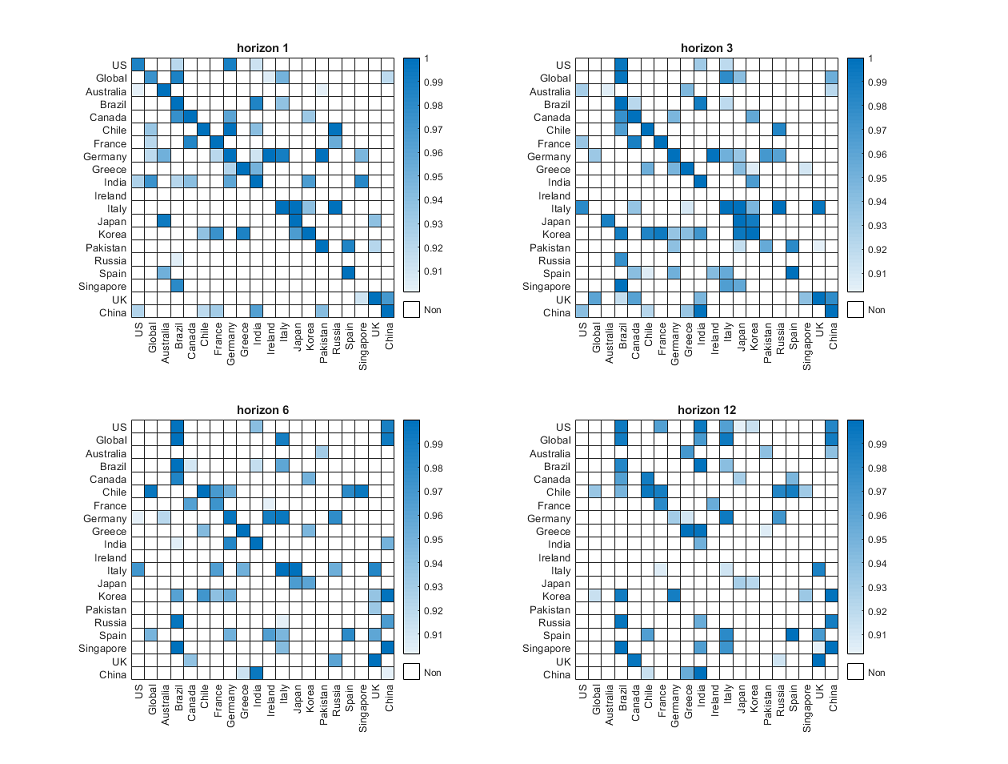
“Causal mechanism and mediation analysis for macroeconomics dynamics” with Jean-Marie Dufour (McGill University). April 2024, 32 pages.
previous title “Intervention analysis, causality and generalized impulse responses in VAR models: theory and inference”
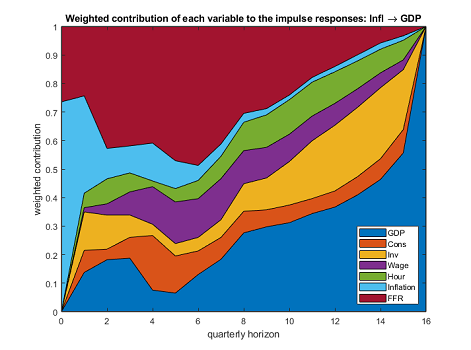
In macroeconomic dynamics, a primary objective is to disentangle the contribution of individual variables in the causal transmission of exogenous interventions across multiple horizons. This paper introduces an innovative index that quantitatively measures the weighted contribution of variables during the propagation of a structural shock over time, offering researchers a perspicuous understanding of the causal transmission mechanisms. The index is based on the novel concept of ‘impulse response decomposition,’ which shows that the impulse response is attributed to the systematic responses of endogenous variables influenced by the initial shock. We employ a counterfactual exercise to evaluate the index under the scenario that the variable of interest has no mediation effect on the output variable in the shock propagation. We apply our channel index to quantify the dynamic contribution of each variable in an inflation shock transmission, thereby illuminating the causal mechanism of inflation on output.
Work in Progress
“Estimation and inference on time-varying impulse responses in high dimensional state-dependent VAR”
This paper introduces an innovative estimation method and derives asymptotic inferences for time-varying impulse responses in a high-dimensional (HD), state-dependent VAR model. Traditional approaches based on nonlinear HD Local Projection (HDLP) methods lack solid theoretical justification, particularly regarding the potential non-equivalence between recursive VAR and the Local Projection method in nonlinear contexts. In contrast, our methodology is firmly grounded in the state-dependent VAR framework. We also address the challenge of asymptotic bias in impulse response estimation within high-dimensional settings. To mitigate this bias, we propose a moment-based pseudo-local projection method that estimates time-varying impulse responses while correcting for biases arising from penalized estimation. Overall, we provide de-biased time-varying impulse responses with asymptotic Gaussian inferences. The methodology is supported by Monte Carlo simulations, and we demonstrate its application in two macroeconomic contexts: monetary policy and government spending.“Generic identification and practical specification for multivariate time series”
This paper introduces a novel identification condition for vector autoregressive moving-average (VARMA) processes based on the second moments of the explanatory variables. The proposed condition supports a wide range of commonly used VARMA representations, including the Echelon form, Scalar Component model, and Diagonal (final) equation form. We also present an identified VARMA representation alongside a specification procedure that is both practical and user-friendly. Compared to traditional methods such as the Echelon form, our representation offers greater structural flexibility, enhanced computational efficiency in estimation, and better integration with the structural VARMA framework. The paper features Monte Carlo simulations, a comparison of VARMA and VAR models in terms of impulse response estimation, and an empirical analysis of the dynamic causal effects of monetary policy shocks.“The (mis)-identification and estimation of structural impulse responses in sub-space VAR model”
This paper compares the identification and estimation of impulse responses under a sub-space Vector Autoregression (VAR) framework using Structural VAR (SVAR) and Local Projection (LP) methods with external instruments. A sub-space VAR refers to a situation where the model is selected from a larger VAR system with omitted variables, a well-known issue in microeconometrics but often overlooked in macroeconometrics. Our study contributes to the literature on external instrumental variable estimation of impulse responses by: (1) examining the bias-variance trade-off between SVAR and LP impulse response estimates under a sub-space VAR model; (2) establishing the necessary and sufficient conditions for the equivalence of SVAR and LP impulse response estimands; and (3) proposing a specification test for the validity of external instruments in proxy-SVAR analysis.